Kahneman and Tversky’s “debatable” loss aversion assumption
Loss aversion is the idea that losses loom larger than gains. It is one of the foundational concepts in the judgment and decision making literature. In Thinking, Fast and Slow, Daniel Kahneman wrote “The concept of loss aversion is certainly the most significant contribution of psychology to behavioral economics.”
Yet, over the last couple of years several critiques have emerged that question the foundations of loss aversion and whether loss aversion is a phenomena at all.
One is an article by Eldad Yechiam, titled Acceptable losses: the debatable origins of loss aversion (pdf). Framed in one case as a spread of the replication crisis to loss aversion, the abstract reads as follows:
It is often claimed that negative events carry a larger weight than positive events. Loss aversion is the manifestation of this argument in monetary outcomes. In this review, we examine early studies of the utility function of gains and losses, and in particular the original evidence for loss aversion reported by Kahneman and Tversky (Econometrica 47:263–291, 1979). We suggest that loss aversion proponents have over-interpreted these findings. Specifically, the early studies of utility functions have shown that while very large losses are overweighted, smaller losses are often not. In addition, the findings of some of these studies have been systematically misrepresented to reflect loss aversion, though they did not find it. These findings shed light both on the inability of modern studies to reproduce loss aversion as well as a second literature arguing strongly for it.
A second, The Loss of Loss Aversion: Will It Loom Larger Than Its Gain (pdf), by David Gal and Derek Rucker, attacks the concept of loss aversion more generally (supposedly the “death knell”):
Loss aversion, the principle that losses loom larger than gains, is among the most widely accepted ideas in the social sciences. The first part of this article introduces and discusses the construct of loss aversion. The second part of this article reviews evidence in support of loss aversion. The upshot of this review is that current evidence does not support that losses, on balance, tend to be any more impactful than gains. The third part of this article aims to address the question of why acceptance of loss aversion as a general principle remains pervasive and persistent among social scientists, including consumer psychologists, despite evidence to the contrary. This analysis aims to connect the persistence of a belief in loss aversion to more general ideas about belief acceptance and persistence in science. The final part of the article discusses how a more contextualized perspective of the relative impact of losses versus gains can open new areas of inquiry that are squarely in the domain of consumer psychology.
A third strain of criticism relates to the concept of ergodicity. Put forward by Ole Peters, the basic claim is that people are not maximising the expected value of a series of gambles, but rather the time average. If people maximise the latter, not the former as many approaches assume, you don’t need risk or loss aversion to explain the decisions. (I’ll leave explaining what exactly this means to a later post.)
I’m as sceptical and cynical about the some of the findings in the behavioural sciences as most (here’s my critical behavioural economics and behavioural science reading list), but I’m not sure I am fully on board with these arguments, particularly the stronger statements of Gal and Rucker. This post is the first of a few rummaging through these critiques to make sense of the debate, starting with Yechiam’s paper on the foundations of loss aversion in prospect theory.
Acceptable losses: the debatable origins of loss aversion
One of the most cited papers in the social sciences is Daniel Kahneman and Amos Tversky’s 1979 paper Prospect Theory: An Analysis of Decision under Risk (pdf). Prospect theory is intended to be a descriptive model of how people make decisions under risk, and an alternative to expected utility theory.
Under expected utility theory, people assign a utility value to each possible outcome of a lottery or gamble, with that outcome typically relating to a final level of wealth. The expected utility for a decision under risk is simply the probability weighted sum of these utilities. The utility of a 50% chance of $0 and a 50% chance of $200 is simply the sum of 50% of the utility of each of $0 and $200.
When utility is assumed to increase at a decreasing rate with each additional dollar of additional wealth - as is typically the case - it leads to risk averse behaviour, with a certain sum preferred to a gamble with an equivalent expected value. For example, a risk averse person would prefer $100 for certain that the 50-50 gamble for $0 or $200.
In their 1979 paper, Kahneman and Tversky described a number of departures from expected utility theory. These included:
The certainty effect: People overweight outcomes that are considered certain, relative to outcomes which are merely probable.
The reflection effect: Relative to a reference point, people are risk averse when considering gains, but risk seeking when facing losses.
The isolation effect: People focus on the elements that differ between options rather than those components that are shared.
Loss aversion: Losses loom larger than gains - relative to a reference point, a loss is more painful than a gain of the same magnitude.
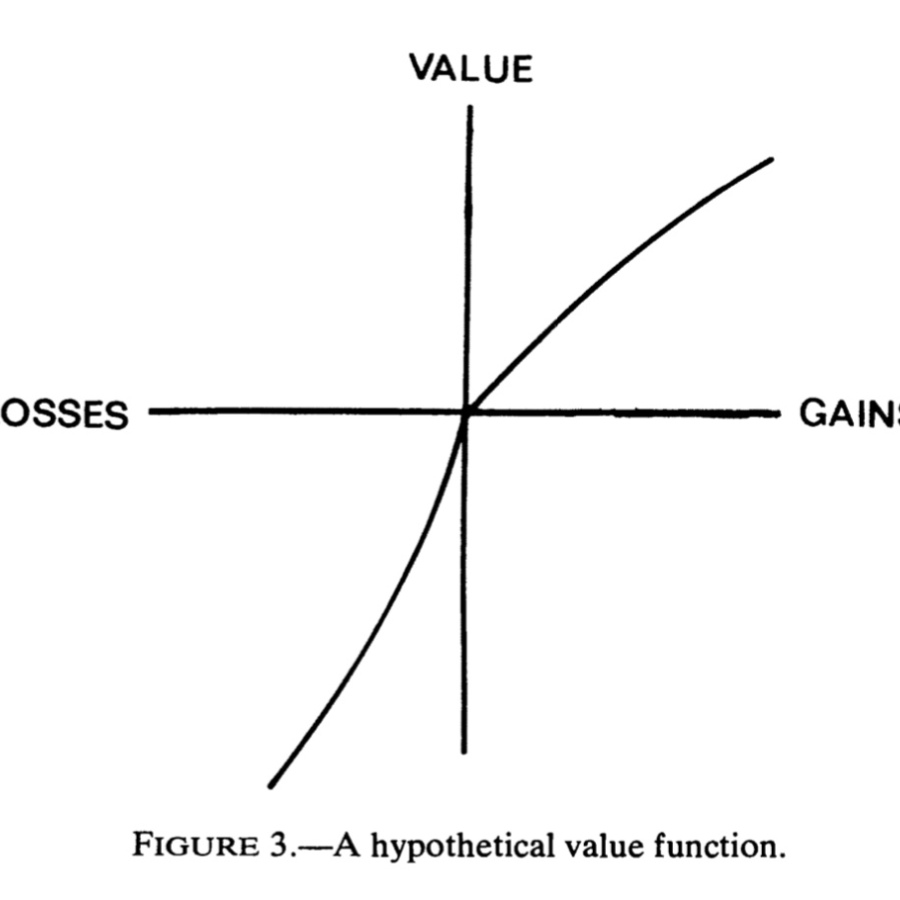
Loss aversion and the reflection effect result in the following famous diagram of how people weight losses and gains under prospect theory. Loss aversion leads to a kink in the utility curve at the reference point. The curve is steeper below the reference point than above. The reflection effect results in the curve being concave above the reference point, and convex below.
Through the paper, Kahneman and Tversky describe experiments on each of the certainty effect, reflection effect, and isolation effect. However, as pointed out by Eldad Yechiam in his paper Acceptable losses: the debatable origins of loss aversion, loss aversion is taken as a stylised fact. Yechiam writes:
[I]n their 1979 paper, Kahneman and Tversky (1979) strongly argued for loss aversion, even though, at the time, they had not reported any experiments to support it. By indicating that this was a robust finding in earlier research, Kahneman and Tversky (1979) were able to rely upon it as a stylized fact. They begin their discussion on losses by stating that “a salient characteristic of attitudes to changes in welfare is that losses loom larger than gains” (p. 279), which suggests that this stylized fact is based on earlier findings. They then follow with the (much cited) sentence that “the aggravation that one experiences in losing a sum of money appears to be greater than the pleasure associated with gaining the same amount [17]” (p. 279). Most people who cite this sentence do so without the end quote of Galenter and Pliner (1974). Galenter and Pliner (1974) are, therefore, the first empirical study used to support the notion of loss aversion.
So what did Galenter and Pliner find? Yechiam writes:
Summing up their findings, Galenter and Pliner (1974) reported as follows: “We now turn to the question of the possible asymmetry of the positive and negative limbs of the utility function. On the basis of intuition and anecdote, one would expect the negative limb of the utility function to decrease more sharply than the positive limb increases… what we have observed if anything is an asymmetry of much less magnitude than would have been expected … the curvature of the function does not change in going from positive to negative” (p. 75).
Thus, our search for the historical foundations of loss aversion turns into a dead end on this particular branch: Galenter and Pliner (1974) did not observe such an asymmetry; and their study was quoted erroneously.
Effectively, the primary reference for the claim that we are loss averse does not support it.
So what other sources did Kahneman and Tversky rely on? Yechiam continues:
They argue that “the main properties ascribed to the value function have been observed in a detailed analysis of von Neumann–Morgenstern utility functions for changes of wealth [14].” (p. 281). The citation refers to Fishburn and Kochenberger’s forthcoming paper (at the time; published 1979). Fishburn and Kochenberger’s (1979) study reviews data of five other papers (Grayson, 1960; Green, 1963; Swalm, 1966; Halter & Dean, 1971; Barnes & Reinmuth, 1976) also cited by Kahneman and Tversky (1979). Summing up all of these findings, Kahneman and Tversky (1979) argue that “with a single exception, utility functions were considerably steeper for losses than for gains.” (p. 281). The “single exception” refers to a single participant who was reported not to show loss aversion, while the remaining one apparently did.
These five studies all involved very small samples, involving a total of 30 subjects.
Yechiam walks through three of the studies. On Swalm (1966):
The results of the 13 individuals examined by Swalm … appear at the first glance to be consistent with an asymmetric utility function implying overweighting of losses compared to gains (i.e., loss aversion). Notice, however, that amounts are in the thousands, such that the smallest amount used was set above $1000 and typically above $5000, because it was derived from the participant’s “planning horizon”. Moreover, for more than half of the participants, the utility curve near the origin …, which spans the two smallest gains and two smallest losses for each person, was linear. This deviates from the notion of loss aversion which implies that asymmetries should also be observed for small amounts as well.
This point reflects an argument that Yechiam and other have made in several papers (including here and here) that loss aversion is only apparent in high-stakes gambles. When the stakes are low, loss aversion does not appear.
On Grayson (1960):
A similar pattern is observed in Grayson’s utility functions … The amounts used were also extreme high, with only one or two points below the $50,000 range. For the points above $100,000, the pattern seems to show a clear asymmetry between gains and losses consistent with loss aversion. However, for 2/9 participants …, the utility curve for the points below 100,000 does not indicate loss aversion, and for 2/9 additional participants no loss aversion is observed for the few points below $50,000. Thus, it appears that in Grayson (1960) and Swalm (1966), almost all participants behaved as if they gave extreme losses more weight than corresponding gains, yet about half of them did not exhibit a similar asymmetry for the lower losses (e.g., below $50,000 in Grayson, 1960).
Again, loss aversion is stronger for extreme losses.
On Green (1963):
… Green (1963) did not examine any losses, making any interpretation concerning loss aversion in this study speculative as it rests on the authors’ subjective impression.
The results from Swalm (1966), Grayson (1960) and Green (1963) covers 26 of the 30 participants aggregated by Fishburn and Kochenberger. Halter and Dean (1971) and Barnes and Reinmuth (1976) only involved two participants each.
So what of other studies that were available to Kahneman and Tversky at the time?
In 1955, Davidson, Siegel, and Suppes conducted an experiment in which participants were presented with heads or tails bets which they could accept or refuse. …
… Outcomes were in cents and ran up to a gain or loss of 50 cents. The results of 15 participants showed that utility curves for gains and losses were symmetric …, with a loss/ gain utility ratio of 1.1 (far below than the 2.25 estimated by Tversky and Kahneman, 1992). The authors also re-analyzed an earlier data set by Mosteller and Nogee (1951) involving bets for amounts ranging from − 30 to 30 cents, and it too showed utility curves that were symmetric for gains and losses.
Lichtenstein (1965) similarly used incentivized bets and small amounts. … Lichtenstein (1965) argued that “The preference for low V [variance] bets indicates that the utility curve for money is not symmetric in its extreme ranges; that is, that large losses appear larger than large wins.” (p. 168). Thus, Lichtenstein (1965) interpreted her findings not as a general aversion to losses (which would include small losses and gains), but only as a tendency to overweight large losses relative to large gains.
… Slovic and Lichtenstein (1968) developed a regression-based approach to examine whether the participants’ willingness to pay (WTP) for a certain lottery is predicted more strongly by the size of its gains or the size of its losses. Their results showed that size of losses predicted WTP more than sizes of gains. … Moreover, in a follow-up study, Slovic (1969) found a reverse effect in hypothetical lotteries: Choices were better predicted by the gain amount than the loss amount. In the same study, he found no difference for incentivized lotteries in this respect.
Similar findings of no apparent loss aversion were observed in studies that used probabilities that are learned from experience (Katz, 1963; Katz, 1964; Myers & Suydam, 1964).
In sum, the evidence for loss aversion at the time of the publication of prospect theory was relatively weak and limited to high-stakes gambles.
As Yechiam notes, Kahneman and Tversky only turned their attention to specifically investigating loss aversion in 1992 - and even there it tended to involve large amounts.
Only in 1992 did Tversky and Kahneman (1992) and Redelmeier and Tversky (1992) start to empirically investigate loss aversion, and when they did, they used either very large amounts (Redelmeier & Tversky, 1992) or the so-called “list method” in which one chooses between lotteries with changing amounts up until choices switch from one alternative to the other (Tversky & Kahneman, 1992). This usage of high amounts would come to characterize most of the literature later arguing for loss aversion (e.g., Redelmeier & Tversky, 1992; Abdellaoui et al., 2007; Rabin & Weizsäcker, 2009) as would be the usage of decisions that are not incentivized (i.e., hypothetical; as discussed below).
I’ll examine the post-1979 evidence in more detail in a future post, but in the interim will note this observation from Yechiam on the more recent experiments.
In a review of the literature, Yechiam and Hochman (2013a) have shown that modern studies of loss aversion seem to be binomially distributed into those who used small or moderate amounts (up to $100) and large amounts (above $500). The former typically find no loss aversion, while the latter do. For example, Yechiam and Hochman (2013a) reviewed 11 studies using decisions from description (i.e., where participants are given exact information regarding the probability of gaining and losing money). From these studies, seven did not find loss aversion and all of them used loss/gain amounts of up to $100. Four did find loss aversion, and three of them used very high amounts (above $500 and typically higher). Thus, the usage of high amounts to produce loss aversion is maintained in modern studies.
The presence of loss aversion for only large stakes gambles raises some interesting questions. In particular, are we actually observing the effect of “minimal requirements”, whereby a loss would push them below some minimum threshold for, say, survival or other basic necessities? (Or at least a heuristic that operates with that intent?) This is a distinct concept from loss aversion as presented in prospect theory.
Finally - and a minor point on the claim that Yechiam’s paper was the beginning of the spread of the replication crisis to loss aversion - there is of course no direct experiment on loss aversion in the initial prospect theory paper to be replicated. A recent replication of the experiments in the 1979 paper had positive results (excepting some mixed results concerning the reflection effect). Replication of the 1979 paper doesn’t, however, resolve provide any evidence on the replicability of loss aversion itself, nor the appropriate interpretation of the experiments.
On that point, in my next post on the topic I’ll turn to some of the alternative explanations for what appears to be loss aversion, particularly the claims of Gal and Rucker that losses do not loom larger than gains.